Black hole information paradox

The first image (silhouette or shadow) of a black hole, taken of the supermassive black hole in M87 with the Event Horizon Telescope, released in April 2019

The black hole information paradox<ref>The short form "ínformation paradox" is also used for the Arrow information paradox.</ref> is an unsolved problem in physics and a paradox that appears when the predictions of quantum mechanics and general relativity are combined. The theory of general relativity predicts the existence of black holes that are regions of spacetime from which nothing—not even light—can escape. In the 1970s, Stephen Hawking applied the semiclassical approach of quantum field theory in curved spacetime to such systems and found that an isolated black hole would emit a form of radiation (now called Hawking radiation in his honor). He also argued that the detailed form of the radiation would be independent of the initial state of the black hole,<ref name="hawkbreak">Template:Cite journal</ref> and depend only on its mass, electric charge and angular momentum.

The information paradox appears when one considers a process in which a black hole is formed through a physical process and then evaporates away entirely through Hawking radiation. Hawking's calculation suggests that the final state of radiation would retain information only about the total mass, electric charge and angular momentum of the initial state. Since many different states can have the same mass, charge and angular momentum, this suggests that many initial physical states could evolve into the same final state. Therefore, information about the details of the initial state would be permanently lost; however, this violates a core precept of both classical and quantum physics: that, in principle only, the state of a system at one point in time should determine its state at any other time.<ref name="SH-2006">Template:Cite video</ref><ref name="NYT-20130812">Template:Cite news</ref> Specifically, in quantum mechanics the state of the system is encoded by its wave function. The evolution of the wave function is determined by a unitary operator, and unitarity implies that the wave function at any instant of time can be used to determine the wave function either in the past or the future. In 1993, Don Page argued that if a black hole starts in a pure quantum state and evaporates completely by a unitary process, the von Neumann entropy of the Hawking radiation initially increases and then decreases back to zero when the black hole has disappeared.<ref name=1993-page>Template:Cite journal</ref> This is called the Page curve.<ref name="CoxForshaw Page-curve">Template:Cite book</ref>

It is now generally believed that information is preserved in black-hole evaporation.<ref name="QT-20201030">Template:Cite news</ref><ref name="entrhawk">Template:Cite journal</ref><ref name="lessons">Template:Cite journal</ref> For many researchers, deriving the Page curve is synonymous with solving the black hole information puzzle.<ref name=GS2022textbook>Template:Cite book</ref>Template:Rp But views differ as to precisely how Hawking's original semiclassical calculation should be corrected.<ref name="entrhawk"/><ref name="lessons"/><ref name="mathurpedag">Template:Cite journal</ref><ref name="bhlqg">Template:Cite journal</ref> In recent years, several extensions of the original paradox have been explored. Taken together, these puzzles about black hole evaporation have implications for how gravity and quantum mechanics must be combined. The information paradox remains an active field of research in quantum gravity.

Relevant principles

In quantum mechanics, the evolution of the state is governed by the Schrödinger equation. The Schrödinger equation obeys two principles that are relevant to the paradox—quantum determinism, which means that given a present wave function, its future changes are uniquely determined by the evolution operator, and reversibility, which refers to the fact that the evolution operator has an inverse, meaning that the past wave functions are similarly unique. The combination of the two means that information must always be preserved.<ref name="sh 2019 0823">Template:Cite web</ref> In this context "information" means all the details of the state, and the statement that information must be preserved means that details corresponding to an earlier time can always be reconstructed at a later time.

Mathematically, the Schrödinger equation implies that the wavefunction at a time t₁ can be related to the wavefunction at a time t₂ by means of a unitary operator. <math display="block"> |\Psi(t_1)\rangle = U(t_1, t_2)|\Psi(t_2)\rangle.</math> Since the unitary operator is bijective, the wavefunction at t₂ can be obtained from the wavefunction at t₁ and vice versa.

The reversibility of time evolution described above applies only at the microscopic level, since the wavefunction provides a complete description of the state. It should not be conflated with thermodynamic irreversibility. A process may appear irreversible if one keeps track only of the system's coarse-grained features and not of its microscopic details, as is usually done in thermodynamics. But at the microscopic level, the principles of quantum mechanics imply that every process is completely reversible.

Starting in the mid-1970s, Stephen Hawking and Jacob Bekenstein put forward theoretical arguments that suggested that black-hole evaporation loses information, and is therefore inconsistent with unitarity. Crucially, these arguments were meant to apply at the microscopic level and suggested that black-hole evaporation is not only thermodynamically but microscopically irreversible. This contradicts the principle of unitarity described above and leads to the information paradox. Since the paradox suggested that quantum mechanics would be violated by black-hole formation and evaporation, Hawking framed the paradox in terms of the "breakdown of predictability in gravitational collapse".<ref name="hawkbreak" />

The arguments for microscopic irreversibility were backed by Hawking's calculation of the spectrum of radiation that isolated black holes emit.<ref name=Hawking>Template:Cite journal</ref> This calculation utilized the framework of general relativity and quantum field theory. The calculation of Hawking radiation is performed at the black hole horizon and does not account for the backreaction of spacetime geometry; for a large enough black hole the curvature at the horizon is small and therefore both these theories should be valid. Hawking relied on the no-hair theorem to arrive at the conclusion that radiation emitted by black holes would depend only on a few macroscopic parameters, such as the black hole's mass, charge, and spin, but not on the details of the initial state that led to the formation of the black hole. In addition, the argument for information loss relied on the causal structure of the black hole spacetime, which suggests that information in the interior should not affect any observation in the exterior, including observations performed on the radiation the black hole emits. If so, the region of spacetime outside the black hole would lose information about the state of the interior after black-hole evaporation, leading to the loss of information.

Today, some physicists believe that the holographic principle (specifically the AdS/CFT duality) demonstrates that Hawking's conclusion was incorrect, and that information is in fact preserved.<ref name=Barbon>Template:Cite journal http://iopscience.iop.org/1742-6596/171/1/012009 p.1: "The most important departure from conventional thinking in recent years, the holographic principle...provides a definition of quantum gravity...[and] guarantees that the whole process is unitary."</ref> Moreover, recent analyses indicate that in semiclassical gravity the information loss paradox cannot be formulated in a self-consistent manner due to the impossibility of simultaneously realizing all of the necessary assumptions required for its formulation.<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref>

Black hole evaporation

Hawking radiation

The Penrose diagram of a black hole which forms, and then completely evaporates away. Time shown on vertical axis from bottom to top; space shown on horizontal axis from left (radius zero) to right (growing radius).

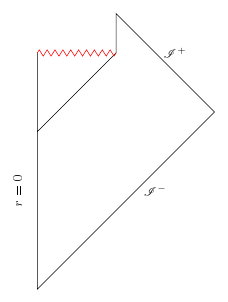
In 1973–1975, Stephen Hawking showed that black holes should slowly radiate away energy, and he later argued that this leads to a contradiction with unitarity. Hawking used the classical no-hair theorem to argue that the form of this radiation—called Hawking radiation—would be completely independent of the initial state of the star or matter that collapsed to form the black hole. He argued that the process of radiation would continue until the black hole had evaporated completely. At the end of this process, all the initial energy in the black hole would have been transferred to the radiation. But, according to Hawking's argument, the radiation would retain no information about the initial state and therefore information about the initial state would be lost.

More specifically, Hawking argued that the pattern of radiation emitted from the black hole would be random, with a probability distribution controlled only by the black hole's initial temperature, charge, and angular momentum, not by the initial state of the collapse. The state produced by such a probabilistic process is called a mixed state in quantum mechanics. Therefore, Hawking argued that if the star or material that collapsed to form the black hole started in a specific pure quantum state, the process of evaporation would transform the pure state into a mixed state. This is inconsistent with the unitarity of quantum-mechanical evolution discussed above.

The loss of information can be quantified in terms of the change in the fine-grained von Neumann entropy of the state. A pure state is assigned a von Neumann entropy of 0, whereas a mixed state has a finite entropy. The unitary evolution of a state according to Schrödinger's equation preserves the entropy. Therefore Hawking's argument suggests that the process of black-hole evaporation cannot be described within the framework of unitary evolution. Although this paradox is often phrased in terms of quantum mechanics, the evolution from a pure state to a mixed state is also inconsistent with Liouville's theorem in classical physics (see e.g.<ref>L. Susskind and J. Lindesay, Black Holes, Information and the String Theory Revolution, World Scientific, 2005, pp. 69-84; Template:ISBN.</ref>).

In equations, Hawking showed that if one denotes the creation and annihilation operators at a frequency <math>\omega</math> for a quantum field propagating in the black-hole background by <math>a_{\omega}</math> and <math>a_{\omega}^{\dagger}</math> then the expectation value of the product of these operators in the state formed by the collapse of a black hole would satisfy <math display="block"> \langle a_{\omega} a_{\omega}^{\dagger} \rangle_{\rm hawk} = {1 \over 1 - e^{-\omega /{kT} }} </math> where Template:Math is the Boltzmann constant and Template:Math is the temperature of the black hole. (See, for example, section 2.2 of.<ref name="lessons" />) This formula has two important aspects. The first is that the form of the radiation depends only on a single parameter, temperature, even though the initial state of the black hole cannot be characterized by one parameter. Second, the formula implies that the black hole radiates mass at a rate given by <math display="block"> {d M \over d t} = -{a T^4}</math> where Template:Math is constant related to fundamental constants, including the Stefan–Boltzmann constant and certain properties of the black hole spacetime called its greybody factors.

The temperature of the black hole is in turn dependent on its mass, charge, and angular momentum. For a Schwarzschild Black Hole the temperature is given by <math display="block"> T = {\hbar c^3 \over 8 \pi k G M} </math> This means that if the black hole starts out with an initial mass <math>M_0</math>, it evaporates completely in a time proportional to <math>M_0^3</math>.

The important aspect of these formulas is that they suggest that the final gas of radiation formed through this process depends only on the black hole's temperature and is independent of other details of the initial state. This leads to the following paradox. Consider two distinct initial states that collapse to form a Schwarzschild black hole of the same mass. Even though the states were distinct at first, since the mass (and hence the temperature) of the black holes is the same, they will emit the same Hawking radiation. Once they evaporate completely, in both cases, one will be left with a featureless gas of radiation. This gas cannot be used to distinguish between the two initial states, and therefore information has been lost.

Page curve

During the same time period in the 1970s, Don Page was a doctoral student of Stephen Hawking. He objected to Hawking's reasoning leading to the paradox above, initially on the basis of violation of CPT symmetry.<ref>Template:Cite journal</ref> In 1993, Page focused on the combined system of a black hole with its Hawking radiation as one entangled system, a bipartite system, evolving over the lifetime of the black hole evaporation. Lacking the ability to make a full quantum analysis, he nonetheless made a powerful observation: If a black hole starts in a pure quantum state and evaporates completely by a unitary process, the von Neumann entropy or entanglement entropy of the Hawking radiation initially increases from zero and then must decrease back to zero when the black hole to which the radiation is entangled has totally evaporated.<ref name="1993-page" /> This is known as the Page curve; and the time corresponding to the maximum or turnover point of the curve, which occurs at about half the black-hole lifetime, is called the Page time.<ref name="Almheiri et al RMP2021">Template:Cite journal</ref> In short, if black hole evaporation is unitary, then the radiation entanglement entropy follows the Page curve. After the Page time, correlations appear and the radiation becomes increasingly information rich.<ref name="CoxForshaw Page-curve" />

Recent progress in deriving the Page curve for unitary black hole evaporation is a significant step towards finding both a resolution to the information paradox and a more general understanding of unitarity in quantum gravity.<ref name="Imseis 2021">Template:Cite web</ref> Many researchers consider deriving the Page curve as synonymous with solving the black hole information paradox.<ref name="GS2022textbook" />Template:Rp

Popular culture

The information paradox has received coverage in the popular media and has been described in popular-science books. Some of this coverage resulted from a widely publicized bet made in 1997 between John Preskill on the one hand with Hawking and Kip Thorne on the other that information was not lost in black holes. The scientific debate on the paradox was described in Leonard Susskind's 2008 book The Black Hole War. (The book carefully notes that the 'war' was purely a scientific one, and that, at a personal level, the participants remained friends.<ref>Template:Cite book</ref>) Susskind writes that Hawking was eventually persuaded that black-hole evaporation was unitary by the holographic principle, which was first proposed by Gerard 't Hooft, further developed by Susskind, and later given a precise string theory interpretation by the AdS/CFT correspondence.<ref>Template:Cite web</ref> In 2004, Hawking also conceded the 1997 bet, paying Preskill with a baseball encyclopedia "from which information can be retrieved at will". Thorne refused to concede.<ref>Template:Cite web</ref>

Solutions

Since the 1997 proposal of the AdS/CFT correspondence, the predominant belief among physicists is that information is indeed preserved in black hole evaporation. There are broadly two main streams of thought about how this happens. Within what might broadly be termed the "string theory community", the dominant idea is that Hawking radiation is not precisely thermal but receives quantum correlations that encode information about the black hole's interior.<ref name="lessons" /> This viewpoint has been the subject of extensive recent research and received further support in 2019 when researchers amended the computation of the entropy of the Hawking radiation in certain models and showed that the radiation is in fact dual to the black hole interior at late times.<ref name="BHInterior">Template:Cite arXiv</ref><ref name="HREntropy">Template:Cite journal</ref> Hawking himself was influenced by this view and in 2004 published a paper that assumed the AdS/CFT correspondence and argued that quantum perturbations of the event horizon could allow information to escape from a black hole, which would resolve the information paradox.<ref name="baezweek207">Template:Cite web</ref> In this perspective, it is the event horizon of the black hole that is important and not the black-hole singularity. The GISR of references<ref name="dfzeng2021">Template:Cite journal</ref><ref name="dfzeng2022">Template:Cite journal</ref> is an implementation of this idea, with the quantum perturbation of event horizon replaced by the microscopic state of black holes.

On the other hand, within what might broadly be termed the "loop quantum gravity community", the dominant belief is that to resolve the information paradox, it is important to understand how the black-hole singularity is resolved. These scenarios are broadly called "remnant scenarios" since information does not emerge gradually but remains in the black-hole interior only to emerge at the end of black-hole evaporation.<ref name="bhlqg" />

Researchers also study other possibilities, including a modification of the laws of quantum mechanics to allow for non-unitary time evolution.

Some of these solutions are described at greater length below.

GISR mechanism resolution to the paradox

This resolution takes the Gravity Induced Spontaneous Radiation as the underlying mechanism for Hawking radiation, whose physics ingredients are written in an explicitly hermitian hamiltonian

<math display="block">\begin{align}

                   H &= \begin{pmatrix}w^i\\&w_{-}^{j}\\&&\ddots\\&&&{\scriptstyle\it0}^{\scriptscriptstyle\it1}\end{pmatrix} + \sum_q\hbar\omega_qa^\dagger_qa_q + \sum_{u,v}^{|u-v|=\hbar\omega_q}g_{u^n v^\ell}b^\dagger_{u^n v^\ell}a_q \\
 g_{u\;\!\!^n v^\ell} &\propto -\frac{\hbar}{G\{M_u,M_v\}^\mathrm{max}}\mathrm{Siml}\{\Psi[M_{u\;\!\!^n}\!(r)],\Psi[M_{v\;\!\!^\ell}\!(r)]\}

\end{align}</math>

The first term on the right hand side is a matrix representation of microscopic states of black holes no heavier than the initial one, each <math>w^i</math> is <math>w</math>-times degenerated. The second term describes the vacuum fluctuation of particles around the black hole. The third term couples the two, so that for each vacuum mode whose energy matches the mass difference between two states of the black hole, transition happens with an amplitude proportional to the similarity factor between the initial and final black hole microcopical state. Transitions from higher energy state <math>w^i</math> to lower energy state <math>w^k_{-\cdots}</math> and the inverse, are equally permitted at the Hamiltonian level. This coupling mimics the photon-atom interaction of Jaynes–Cummings model in atomic physics, replacing the vector potential of photons with the mass-energy of hawking particles, and the dipole moment of initial-to-final transitions in atoms with the similarity factor of initial and final states of black holes.

By the hamiltonian of GISR, evolutions of an evaporating black hole and its hawking particles are controlled by the standard Schrodinger equation,

<math>|\psi(t)\rangle=\sum_{u=w}^0\sum_{n=1}^{u}\sum_{\omega{}s}^{\omega+u=w} e^{-iut-i\omega{}t}c_{u\;\!\!^n}^{\omega{}s}(t)|u\;\!\!^n\otimes\omega{}s\rangle </math>

<math>i\hbar{\partial}_t|\psi(t)\rangle = H|\psi(t)\rangle</math>

where <math>\omega{}s</math> is the index of hawking-particles set with total energy <math>\omega</math>. In the short time evolution or single quantum emission, Wigner-Wiesskopf approximation allows one<ref name="dfzeng2021"/><ref name="dfzeng2022"/> to show that the spectrum of GISR is exactly of thermal type and the corresponding temperature equals to that of Hawking radiation. In the long time evolution or continuous quantum emission, the process is off-equilibrium and is characterised by an initial state dependent black hole mass or temperature vs. time curve. The observers far away can retrieve the information stored in the initial black holes from their mass or temperature v.s. time curve.

The hamiltonian and wave function description of GISR allows the entanglement entropy between the black hole and its Hawking particles be calculated explicitly,

<math>s_{BR} = -\operatorname{tr}_{B}\rho_{B}\log\rho_{B}=-tr_{R} \rho_{R}\log\rho_{R}</math>

<math> \rho_{B} = \operatorname{tr}_{R}\sum_{u=w}^0\sum_{n=1}^{u}\sum_{\omega{}s}^{\omega+u=w}|c_{u^n}^{\omega{}s}\rangle\langle c_{u^n}^{\omega{}s}| </math>

<math> \rho_{R} = \operatorname{tr}_{B}\sum_{u=w}^0\sum_{n=1}^{u}\sum_{\omega{}s}^{\omega+u=w}|c_{u^n}^{\omega{}s}\rangle\langle c_{u^n}^{\omega{}s}| </math>

Since the Hamiltonian of GISR is explicitly Hermitian, the first increasing then decreasing feature feature of the resultant entropy is naturally obtained. What the calculation tells us is that, the intermediate state of an evaporating black hole cannot be considered a semiclassical object with a time-dependent mass. Instead, it should be viewed as a superposition of many different mass ratio combinations of partially radiated black holes and Hawking particles. References<ref name="dfzeng2021"/><ref name="dfzeng2022"/> designed a Schrödinger cat-type thought experiment to illustrate this fact, where an initial black hole is bind with a group of living cats and each Hawking particle kills one from the group. In a quantum description, because the time and number of hawking particles being radiated cannot be determined definitively, the intermediate state of an evaporating black hole can only be considered a superposition of many cat groups, each with a different ratio of dead members. The most significant flaw in the argument for information loss is the neglect of this superposition.

Small-corrections resolution to the paradox

This idea suggests that Hawking's computation fails to keep track of small corrections that are eventually sufficient to preserve information about the initial state.<ref name="giddings1995"/><ref name="preskill1992"/><ref name="lessons" /> This can be thought of as analogous to what happens during the mundane process of "burning": the radiation produced appears to be thermal, but its fine-grained features encode the precise details of the object that was burnt. This idea is consistent with reversibility, as required by quantum mechanics. It is the dominant idea in what might broadly be termed the string-theory approach to quantum gravity.

More precisely, this line of resolution suggests that Hawking's computation is corrected so that the two point correlator computed by Hawking and described above becomes <math display="block"> \langle a_{\omega} a_{\omega}^{\dagger} \rangle_{\rm exact} = \langle a_{\omega} a_{\omega}^{\dagger} \rangle_{\rm hawk} (1 + \epsilon_2) </math> and higher-point correlators are similarly corrected <math display="block"> \langle a_{\omega_1} a_{\omega_1}^{\dagger} a_{\omega_2} a_{\omega_2}^{\dagger} \ldots a_{\omega_n} a_{\omega_n}^{\dagger} \rangle_{\rm exact} = \langle a_{\omega} a_{\omega}^{\dagger} \rangle_{\rm hawk} (1 + \epsilon_n) </math> The equations above utilize a concise notation and the correction factors <math>\epsilon_i</math> may depend on the temperature, the frequencies of the operators that enter the correlation function and other details of the black hole.

Maldacena initially explored such corrections in a simple version of the paradox.<ref name="maldetern">Template:Cite journal</ref> They were then analyzed by Papadodimas and Raju,<ref name ="infalling">Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite journal</ref> who showed that corrections to low-point correlators (such as <math>\epsilon_2</math> above ) that were exponentially suppressed in the black-hole entropy were sufficient to preserve unitarity, and significant corrections were required only for very high-point correlators. The mechanism that allowed the right small corrections to form was initially postulated in terms of a loss of exact locality in quantum gravity so that the black-hole interior and the radiation were described by the same degrees of freedom. Recent developments suggest that such a mechanism can be realized precisely within semiclassical gravity and allows information to escape.<ref name="entrhawk" /> See § Recent developments.

Fuzzball resolution to the paradox

Some researchers, most notably Samir Mathur, have argued<ref name="mathurpedag" /> that the small corrections required to preserve information cannot be obtained while preserving the semiclassical form of the black-hole interior and instead require a modification of the black-hole geometry to a fuzzball.<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite journal</ref>

The defining characteristic of the fuzzball is that it has structure at the horizon scale. This should be contrasted with the conventional picture of the black-hole interior as a largely featureless region of space. For a large enough black hole, tidal effects are very small at the black-hole horizon and remain small in the interior until one approaches the black-hole singularity. Therefore, in the conventional picture, an observer who crosses the horizon may not even realize they have done so until they start approaching the singularity. In contrast, the fuzzball proposal suggests that the black hole horizon is not empty. Consequently, it is also not information-free, since the details of the structure at the surface of the horizon preserve information about the black hole's initial state. This structure also affects the outgoing Hawking radiation and thereby allows information to escape from the fuzzball.

The fuzzball proposal is supported by the existence of a large number of gravitational solutions called microstate geometries.<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite book</ref><ref>Template:Cite journal</ref><ref>Template:Cite journal</ref>

The firewall proposal can be thought of as a variant of the fuzzball proposal that posits that the black-hole interior is replaced by a firewall rather than a fuzzball. Operationally, the difference between the fuzzball and the firewall proposals has to do with whether an observer crossing the horizon of the black hole encounters high-energy matter, suggested by the firewall proposal, or merely low-energy structure, suggested by the fuzzball proposal. The firewall proposal also originated with an exploration of Mathur's argument that small corrections are insufficient to resolve the information paradox.<ref name="mathurpedag" />

The fuzzball and firewall proposals have been questioned for lacking an appropriate mechanism that can generate structure at the horizon scale.<ref name="lessons" />

Strong-quantum-effects resolution to the paradox

In the final stages of black-hole evaporation, quantum effects become important and cannot be ignored. The precise understanding of this phase of black-hole evaporation requires a complete theory of quantum gravity. Within what might be termed the loop-quantum-gravity approach to black holes, it is believed that understanding this phase of evaporation is crucial to resolving the information paradox.

This perspective holds that Hawking's computation is reliable until the final stages of black-hole evaporation, when information suddenly escapes.<ref name="giddings1995"/><ref name="preskill1992"/><ref>Template:Cite journal</ref><ref name="bhlqg" /> Another possibility along the same lines is that black-hole evaporation simply stops when the black hole becomes Planck-sized. Such scenarios are called "remnant scenarios".<ref name="giddings1995"/><ref name="preskill1992"/>

An appealing aspect of this perspective is that a significant deviation from classical and semiclassical gravity is needed only in the regime in which the effects of quantum gravity are expected to dominate. On the other hand, this idea implies that just before the sudden escape of information, a very small black hole must be able to store an arbitrary amount of information and have a very large number of internal states. Therefore, researchers who follow this idea must take care to avoid the common criticism of remnant-type scenarios, which is that they might may violate the Bekenstein bound and lead to a violation of effective field theory due to the production of remnants as virtual particles in ordinary scattering events.<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref>

Soft-hair resolution to the paradox

In 2016, Hawking, Perry and Strominger noted that black holes must contain "soft hair".<ref name=SciAm2016>Template:Cite web</ref><ref name=Hawking2016>Template:Cite journal</ref><ref>Template:Cite web</ref> Particles that have no rest mass, like photons and gravitons, can exist with arbitrarily low-energy and are called soft particles. The soft-hair resolution posits that information about the initial state is stored in such soft particles. The existence of such soft hair is a peculiarity of four-dimensional asymptotically flat space and therefore this resolution to the paradox does not carry over to black holes in Anti-de Sitter space or black holes in other dimensions.

Information is irretrievably lost

A minority view in the theoretical physics community is that information is genuinely lost when black holes form and evaporate.<ref name="giddings1995">Template:Cite conference</ref><ref name="preskill1992">Template:Cite conference</ref> This conclusion follows if one assumes that the predictions of semiclassical gravity and the causal structure of the black-hole spacetime are exact.

But this conclusion leads to the loss of unitarity. Banks, Susskind and Peskin argue that, in some cases, loss of unitarity also implies violation of energy–momentum conservation or locality, but this argument may possibly be evaded in systems with a large number of degrees of freedom.<ref name="nikolic_JCAP2015">Template:Cite journal</ref> According to Roger Penrose, loss of unitarity in quantum systems is not a problem: quantum measurements are by themselves already non-unitary. Penrose claims that quantum systems will in fact no longer evolve unitarily as soon as gravitation comes into play, precisely as in black holes. The Conformal Cyclic Cosmology Penrose advocates critically depends on the condition that information is in fact lost in black holes. This new cosmological model might be tested experimentally by detailed analysis of the cosmic microwave background radiation (CMB): if true, the CMB should exhibit circular patterns with slightly lower or slightly higher temperatures. In November 2010, Penrose and V. G. Gurzadyan announced they had found evidence of such circular patterns in data from the Wilkinson Microwave Anisotropy Probe (WMAP), corroborated by data from the BOOMERanG experiment.<ref>Template:Cite arXiv</ref> The significance of these findings was debated.<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite arXiv</ref>

Along similar lines, Modak, Ortíz, Peña, and Sudarsky have argued that the paradox can be dissolved by invoking foundational issues of quantum theory often called the measurement problem of quantum mechanics.<ref>Template:Cite journal</ref> This work built on an earlier proposal by Okon and Sudarsky on the benefits of objective collapse theory in a much broader context.<ref>Template:Cite journal</ref> The original motivation of these studies was Penrose's long-standing proposal wherein collapse of the wave-function is said to be inevitable in the presence of black holes (and even under the influence of gravitational field).<ref>Template:Cite book</ref><ref>Template:Cite journal</ref> Experimental verification of collapse theories is an ongoing effort.<ref>Template:Cite journal</ref>

Other proposed resolutions

Some other resolutions to the paradox have also been explored. These are listed briefly below.

• Information is stored in a large remnant<ref name="giddings1992">Template:Cite journal</ref><ref name="nikolic_MPLA2015">Template:Cite journal</ref>Template:ParagraphThis idea suggests that Hawking radiation stops before the black hole reaches the Planck size. Since the black hole never evaporates, information about its initial state can remain inside the black hole and the paradox disappears. But there is no accepted mechanism that would allow Hawking radiation to stop while the black hole remains macroscopic.
• Information is stored in a baby universe that separates from our own universe.<ref name="preskill1992"/><ref>Template:Cite journal</ref>Template:ParagraphSome models of gravity, such as the Einstein–Cartan theory of gravity, which extends general relativity to matter with intrinsic angular momentum (spin), predict the formation of such baby universes. No violation of known general principles of physics is needed. There are no physical constraints on the number of the universes, even though only one remains observable.Template:ParagraphThe Einstein–Cartan theory is difficult to test because its predictions are significantly different from general-relativistic ones only at extremely high densities.
• Information is encoded in the correlations between future and past<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref>Template:ParagraphThe final-state proposal<ref>Template:Cite journal</ref> suggests that boundary conditions must be imposed at the black-hole singularity, which, from a causal perspective, is to the future of all events in the black-hole interior. This helps reconcile black-hole evaporation with unitarity but contradicts the intuitive idea of causality and locality of time-evolution.
• Quantum-channel theoryTemplate:ParagraphIn 2014, Chris Adami argued that analysis using quantum channel theory causes any apparent paradox to disappear; Adami rejects black hole complementarity, arguing instead that no space-like surface contains duplicated quantum information.<ref name="Bradler">Template:Cite journal</ref><ref>Template:Cite journal</ref>

See also

• AdS/CFT correspondence
• Beyond black holes
• Black hole complementarity
• Cosmic censorship hypothesis
• Firewall (physics)
• Fuzzball (string theory)
• Holographic principle
• List of paradoxes
• Maxwell's demon
• No-hair theorem
• No-hiding theorem
• Thorne–Hawking–Preskill bet

External links

• Black Hole Information Loss Problem, a USENET physics FAQ page
• Template:Cite arXiv. Discusses methods of attack on the problem, and their apparent shortcomings.
• Template:Cite journal Report on Hawking's 2004 theory in Nature.
• Template:Cite journal Stephen Hawking's purported solution to the black hole unitarity paradox.
• Hawking and unitarity: a July 2005 discussion of the information loss paradox and Stephen Hawking's role in it
• The Hawking Paradox - BBC Horizon documentary (2005)
• Template:IMDb title
• A Black Hole Mystery Wrapped in a Firewall Paradox