Orthorhombic crystal system

Template:Short description In crystallography, the orthorhombic crystal system is one of the seven crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.

Bravais lattices

There are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.

Bravais lattice	Primitive orthorhombic	Base-centered orthorhombic	Body-centered orthorhombic	Face-centered orthorhombic
Pearson symbol	oP	oS	oI	oF
Unit cell	Orthohombic, simple	Orthohombic, base-centered	Orthohombic, body-centered	Orthohombic, face-centered

For the base-centered orthorhombic lattice, the primitive cell has the shape of a right rhombic prism;<ref>See Template:Harvp, row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90°</ref> it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. Note that the length <math>a</math> of the primitive cell below equals <math>\frac{1}{2} \sqrt{a^2+b^2}</math> of the conventional cell above.

Crystal classes

Template:Further The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,<ref name="ITC">Template:Cite book</ref> orbifold notation, type, and space groups are listed in the table below.

[[Space group#Notation|Template:Abbr]]	Point group					Type	Example	Space groups
	Name<ref>Template:Cite web</ref>	Schön.	Intl	Orb.	Cox.			Primitive	Base-centered	Face-centered	Body-centered
16–24	Rhombic disphenoidal	D2 (V)	222	222	[2,2]+	Enantiomorphic	Epsomite Boron (gamma form)	P222, P2221, P21212, P212121	C2221, C222	F222	I222, I212121
25–46	Rhombic pyramidal	C2v	mm2	*22	[2]	Polar	Hemimorphite, bertrandite	Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2	Cmm2, Cmc21, Ccc2 Amm2, Aem2, Ama2, Aea2	Fmm2, Fdd2	Imm2, Iba2, Ima2
47–74	Rhombic dipyramidal	D2h (Vh)	mmm	*222	[2,2]	Centrosymmetric	Olivine, aragonite, marcasite	Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma	Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce	Fmmm, Fddd	Immm, Ibam, Ibca, Imma

In two dimensions

Template:Main In two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular.

Bravais lattice	Rectangular	Centered rectangular
Pearson symbol	op	oc
Unit cell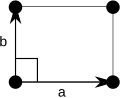

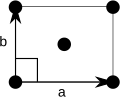
See also

• Crystal structure
• Crystal system
• Overview of all space groups

Further reading

• Template:Cite book
• Template:Cite book