Polygonal number
Template:Short description In mathematics, a polygonal number is a number that counts dots arranged in the shape of a regular polygon.Template:R These are one type of 2-dimensional figurate numbers.
Polygonal numbers were first studied during the 6th century BC by the Ancient Greeks, who investigated and discussed properties of oblong, triangular, and square numbers.Template:R
Definition and examples
The number 10 for example, can be arranged as a triangle (see triangular number):
But 10 cannot be arranged as a square. The number 9, on the other hand, can be (see square number):
Some numbers, like 36, can be arranged both as a square and as a triangle (see square triangular number):
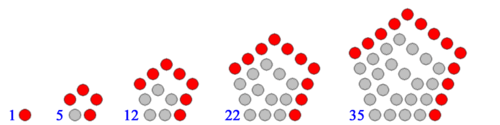
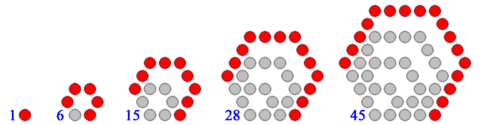
By convention, 1 is the first polygonal number for any number of sides. The rule for enlarging the polygon to the next size is to extend two adjacent arms by one point and to then add the required extra sides between those points. In the following diagrams, each extra layer is shown as in red.
Triangular numbers
The triangular number sequence is the representation of the numbers in the form of equilateral triangle arranged in a series or sequence. These numbers are in a sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45, and so on.
Square numbers
Polygons with higher numbers of sides, such as pentagons and hexagons, can also be constructed according to this rule, although the dots will no longer form a perfectly regular lattice like above.
Pentagonal numbers
Hexagonal numbers
Formula

If Template:Mvar is the number of sides in a polygon, the formula for the Template:Mvarth Template:Mvar-gonal number Template:Math is
- <math>P(s,n) = \frac{(s-2)n^2-(s-4)n}{2}</math>
The Template:Mvarth Template:Mvar-gonal number is also related to the triangular numbers Template:Math as follows:<ref name=":0">Template:Cite book</ref>
- <math>P(s,n) = (s-2)T_{n-1} + n = (s-3)T_{n-1} + T_n\, .</math>
Thus:
- <math>\begin{align}
P(s,n+1)-P(s,n) &= (s-2)n + 1\, ,\\ P(s+1,n) - P(s,n) &= T_{n-1} = \frac{n(n-1)}{2}\, ,\\ P(s+k,n) - P(s,n) &= k T_{n-1} = k\frac{n(n-1)}{2}\, . \end{align}</math>
For a given Template:Mvar-gonal number Template:Math, one can find Template:Mvar by
- <math>n = \frac{\sqrt{8(s-2)x+{(s-4)}^2}+(s-4)}{2(s-2)}</math>
and one can find Template:Mvar by
- <math>s = 2+\frac{2}{n}\cdot\frac{x-n}{n-1}</math>.
Every hexagonal number is also a triangular number
Template:CSS image crop Applying the formula above:
- <math>P(s,n) = (s-2)T_{n-1} + n </math>
to the case of 6 sides gives:
- <math>P(6,n) = 4T_{n-1} + n </math>
but since:
- <math>T_{n-1} = \frac{n(n-1)}{2} </math>
it follows that:
- <math>P(6,n) = \frac{4n(n-1)}{2} + n = \frac{2n(2n-1)}{2} = T_{2n-1}</math>
This shows that the Template:Mvarth hexagonal number Template:Math is also the Template:Mathth triangular number Template:Math. We can find every hexagonal number by simply taking the odd-numbered triangular numbers:<ref name=":0" />
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, ...
Table of values
The first six values in the column "sum of reciprocals", for triangular to octagonal numbers, come from a published solution to the general problem, which also gives a general formula for any number of sides, in terms of the digamma function.<ref name="siam_07-003s">Template:Cite web</ref>
The On-Line Encyclopedia of Integer Sequences eschews terms using Greek prefixes (e.g., "octagonal") in favor of terms using numerals (i.e., "8-gonal").
A property of this table can be expressed by the following identity (see Template:OEIS link):
- <math>2\,P(s,n) = P(s+k,n) + P(s-k,n),</math>
with
- <math>k = 0, 1, 2, 3, ..., s-3.</math>
Combinations
Some numbers, such as 36 which is both square and triangular, fall into two polygonal sets. The problem of determining, given two such sets, all numbers that belong to both can be solved by reducing the problem to Pell's equation. The simplest example of this is the sequence of square triangular numbers.
The following table summarizes the set of Template:Mvar-gonal Template:Mvar-gonal numbers for small values of Template:Mvar and Template:Mvar.
Template:Mvar Template:Mvar Sequence OEIS number 4 3 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, 55420693056, 1882672131025, 63955431761796, 2172602007770041, 73804512832419600, 2507180834294496361, 85170343853180456676, 2893284510173841030625, 98286503002057414584576, 3338847817559778254844961, ... Template:OEIS link 5 3 1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465, … Template:OEIS link 5 4 1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801, ... Template:OEIS link 6 3 All hexagonal numbers are also triangular. Template:OEIS link 6 4 1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625, 3338847817559778254844961, 3853027488179473932250054441, ... Template:OEIS link 6 5 1, 40755, 1533776805, … Template:OEIS link 7 3 1, 55, 121771, 5720653, 12625478965, 593128762435, 1309034909945503, 61496776341083161, 135723357520344181225, 6376108764003055554511, 14072069153115290487843091, … Template:OEIS link 7 4 1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449, 9976444135331412025, … Template:OEIS link 7 5 1, 4347, 16701685, 64167869935, … Template:OEIS link 7 6 1, 121771, 12625478965, … Template:OEIS link 8 3 1, 21, 11781, 203841, … Template:OEIS link 8 4 1, 225, 43681, 8473921, 1643897025, 318907548961, 61866420601441, 12001766689130625, 2328280871270739841, 451674487259834398561, 87622522247536602581025, 16998317641534841066320321, … Template:OEIS link 8 5 1, 176, 1575425, 234631320, … Template:OEIS link 8 6 1, 11781, 113123361, … Template:OEIS link 8 7 1, 297045, 69010153345, … Template:OEIS link 9 3 1, 325, 82621, 20985481, … Template:OEIS link 9 4 1, 9, 1089, 8281, 978121, 7436529, 878351769, 6677994961, 788758910641, 5996832038649, 708304623404049, 5385148492712041, 636056763057925561, ... Template:OEIS link 9 5 1, 651, 180868051, … Template:OEIS link 9 6 1, 325, 5330229625, … Template:OEIS link 9 7 1, 26884, 542041975, … Template:OEIS link 9 8 1, 631125, 286703855361, … Template:OEIS link
In some cases, such as Template:Math and Template:Math, there are no numbers in both sets other than 1.Template:Citation needed
The problem of finding numbers that belong to three polygonal sets is more difficult. Katayama<ref>Template:Cite journal</ref> proved that if three different integers Template:Mvar, Template:Mvar, and Template:Mvar are all at least 3 and not equal to 6, then only finitely many numbers are simultaneously Template:Mvar-gonal, Template:Mvar-gonal, and Template:Mvar-gonal.
Katayama, Furuya, and Nishioka<ref>Template:Cite journal</ref> proved that if the integer Template:Mvar is such that <math>s=5</math> or <math>7\le s\le 12</math>, then the only Template:Mvar-gonal square triangular number is 1. For example, that paper gave the following proof for the case where <math>s=5</math>.<ref>Ibid., p. 4.</ref> Suppose that <math>P(3,n)=P(4,p)=P(5,q)</math> for some positive integers Template:Mvar, Template:Mvar, and Template:Mvar. A calculation shows that the point <math>(x,y)</math> defined by <math>(x,y)=(48p^{2}+3,24p(2n+1)(6q-1))</math> is on the curve <math>Y^{2}=X^{3}-X^{2}-9X+9</math>. That fact forces <math>(x,y)=(51,360)</math> (as an elliptic curve database<ref>Template:Cite web</ref> confirms), so <math>p=1</math> and the result follows.
The number 1225 is hecatonicositetragonal (Template:Math), hexacontagonal (Template:Math), icosienneagonal (Template:Math), hexagonal, square, and triangular.
See also
Notes
References
Bibliography
- The Penguin Dictionary of Curious and Interesting Numbers, David Wells (Penguin Books, 1997) [[[:Template:Isbn]]].
- Template:PlanetMath
- Template:MathWorld
- Template:Cite book
External links
- Template:Springer
- Polygonal Numbers: Every s-polygonal number between 1 and 1000 clickable for 2<=s<=337
- Template:YouTube
- Polygonal Number Counting Function
Template:Classes of natural numbers Template:Series (mathematics) Template:Authority control