Rhombic triacontahedron
Template:Short description Template:More footnotes needed Template:Use dmy dates Template:Infobox polyhedron
The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron and can be seen as an elongated rhombic icosahedron.


The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio, Template:Mvar, so that the acute angles on each face measure Template:Math, or approximately 63.43°. A rhombus so obtained is called a golden rhombus.
Being the dual of an Archimedean solid, the rhombic triacontahedron is face-transitive, meaning the symmetry group of the solid acts transitively on the set of faces. This means that for any two faces, Template:Mvar and Template:Mvar, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face Template:Mvar to face Template:Mvar.
The rhombic triacontahedron is somewhat special in being one of the nine edge-transitive convex polyhedra, the others being the five Platonic solids, the cuboctahedron, the icosidodecahedron, and the rhombic dodecahedron.
The rhombic triacontahedron is also interesting in that its vertices include the arrangement of four Platonic solids. It contains ten tetrahedra, five cubes, an icosahedron and a dodecahedron. The centers of the faces contain five octahedra.
It can be constructed by attaching a right triangular pyramid to each face of a regular icosahedron, of a height such that the adjacent faces of different pyramids are coplanar.<ref name="coplanarity">This happens when the apex height of each pyramid is <math>s\left(\dfrac{3\sqrt{3}-\sqrt{15}}{12}\right)</math>, where <math>s</math> is the edge length of the icosahedron.</ref> It can also be made from a truncated octahedron by dividing the hexagonal faces into three rhombi:

Cartesian coordinates
Let Template:Mvar be the golden ratio. The 12 points given by Template:Math and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the 8 points Template:Math together with the 12 points Template:Math and cyclic permutations of these coordinates. All 32 points together are the vertices of a rhombic triacontahedron centered at the origin. The length of its edges is Template:Math. Its faces have diagonals with lengths Template:Math and Template:Math.
Dimensions
If the edge length of a rhombic triacontahedron is Template:Mvar, surface area, volume, the radius of an inscribed sphere (tangent to each of the rhombic triacontahedron's faces) and midradius, which touches the middle of each edge are:<ref>Stephen Wolfram, "[1]" from Wolfram Alpha. Retrieved 7 January 2013.</ref>
- <math>\begin{align}
S &= 12\sqrt{5}\,a^2 &&\approx 26.8328 a^2 \\[6px] V &= 4\sqrt{5+2\sqrt{5}}\,a^3 &&\approx 12.3107 a^3 \\[6px] r_\mathrm{i} &= \frac{\varphi^2}{\sqrt{1 + \varphi^2}}\,a = \sqrt{1 + \frac{2}{\sqrt{5}}}\,a &&\approx 1.37638 a \\[6px] r_\mathrm{m} &= \left(1+\frac{1}{\sqrt{5}}\right)\,a &&\approx 1.44721 a \end{align}</math>
where Template:Mvar is the golden ratio.
The insphere is tangent to the faces at their face centroids. Short diagonals belong only to the edges of the inscribed regular dodecahedron, while long diagonals are included only in edges of the inscribed icosahedron.
Dissection
The rhombic triacontahedron can be dissected into 20 golden rhombohedra: 10 acute ones and 10 obtuse ones.<ref>Template:Cite web</ref><ref>Dissection of the rhombic triacontahedron</ref>
| 10 | 10 |
|---|---|
 Acute form |
 Obtuse form |
Orthogonal projections
The rhombic triacontahedron has four symmetry positions, two centered on vertices, one mid-face, and one mid-edge. Embedded in projection "10" are the "fat" rhombus and "skinny" rhombus which tile together to produce the non-periodic tessellation often referred to as Penrose tiling.
| Projective symmetry |
[2] | [2] | [6] | [10] |
|---|---|---|---|---|
| Image | 
|

|

|

|
| Dual image |

|
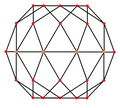
|

|

|
Stellations
Template:Further The rhombic triacontahedron has 227 fully supported stellations.Template:SfnpTemplate:Sfnp One of the stellations of the rhombic triacontahedron is the compound of five cubes, which is represents a regular compound polyhedron. The total number of stellations of the rhombic triacontahedron is Template:Val.
In Dual Models, Magnus Wenninger describes stellations to infinity, hemipolyhedral duals of which the rhombic triacontahedron is the convex hull of three (the small icosihemidodecacron, great dodecahemidodecacron, great dodecahemicosacron). Their boundless faces and edges as elongated prisms or pyramids are orthogonal to the central planes and faces of their dual hemipolyhedra; the coincidental figures of these formed by their corresponding dual hemipolyhedra also have the rhombic triacontahedron as their convex hull.Template:Sfnp
Related polyhedra
Template:Icosahedral truncations
This polyhedron is a part of a sequence of rhombic polyhedra and tilings with Template:Math Coxeter group symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are also rectangles. Template:Dual quasiregular3 table
-
Spherical rhombic triacontahedron
-
A rhombic triacontahedron with an inscribed tetrahedron (red) and cube (yellow).
(Click here for rotating model) -
A rhombic triacontahedron with an inscribed dodecahedron (blue) and icosahedron (purple).
(Click here for rotating model) -
Fully truncated rhombic triacontahedron
Uses
Danish designer Holger Strøm uses the rhombic triacontahedron as a basis for the design of his buildable lamp IQ-light (IQ for "interlocking quadrilaterals").<ref>Template:Cite web</ref>
Woodworker Jane Kostick builds boxes in the shape of a rhombic triacontahedron.<ref>triacontahedron box - KO Sticks LLC</ref> The simple construction is based on the less than obvious relationship between the rhombic triacontahedron and the cube.
Roger von Oech's "Ball of Whacks" comes in the shape of a rhombic triacontahedron.
The rhombic triacontahedron is used as the "d30" thirty-sided die, sometimes useful in some roleplaying games or other places.
See also
References
<references />
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, Template:Isbn [2] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, p. 285, Rhombic triacontahedron )
- Template:Cite journal
- Template:Citation
- Template:Citation (The thirteen semiregular convex polyhedra and their duals, p. 22, Rhombic triacontahedron)
- Template:The Geometrical Foundation of Natural Structure (book) (Section 3-9)
External links
- Stellations of the Rhombic Triacontahedron by George W. Hart (Virtual Polyhedra)
- Art: Stellations of Rhombic Triacontahedron by Vladimir Bulatov (Bulatorv Abstract Creations)
- 120 Rhombic Triacontahedra by Sándor Kabai for The Wolfram Demonstrations Project
Template:Polyhedra Template:Catalan solids Template:Polyhedron navigator

